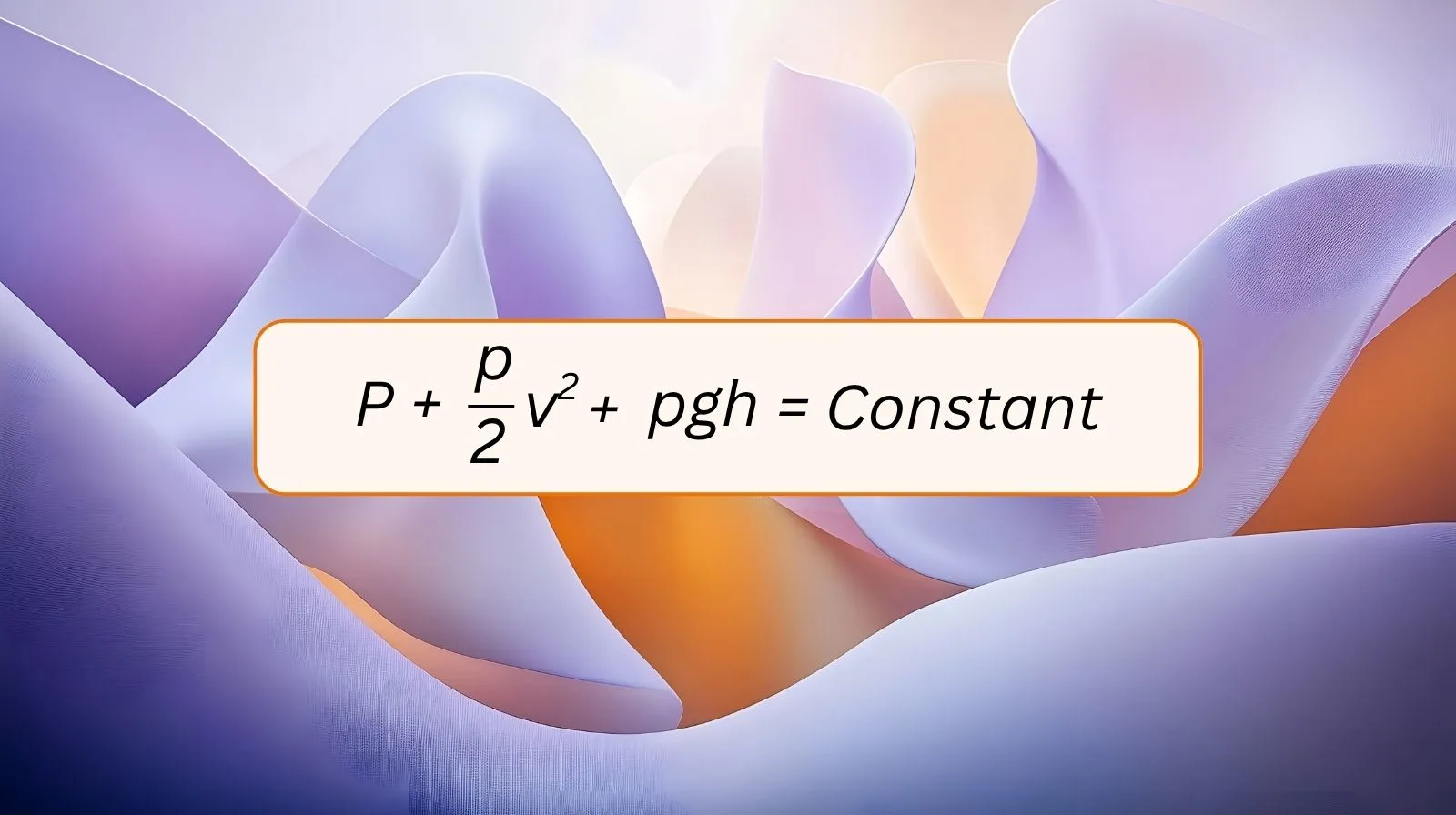Fluids like water and air carry energy when they move. This energy can appear as pressure, speed, or height.
Table of Contents
ToggleDaniel Bernoulli, a scientist in the 18th century, explained how these forms of energy stay balanced in a moving fluid. This idea is known as Bernoulli’s Equation and it is one of the most important principles in fluid mechanics.
It is widely used in designing aircraft wings, pumps, venturi meters and many other engineering systems.
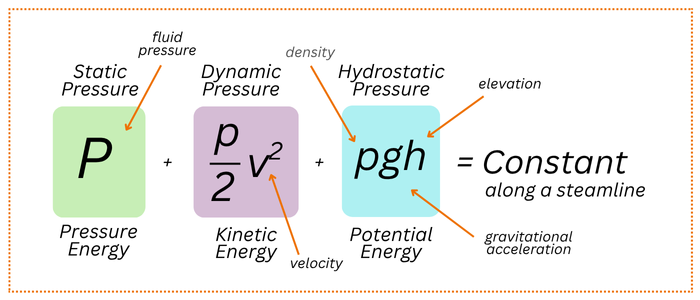
Imagine a fluid moving smoothly through a pipe. Along its path, the fluid carries three types of energy: pressure energy (the push of the fluid), kinetic energy (the energy from its speed), and potential energy (the effect of its height).
Bernoulli’s Equation says: no matter how the fluid moves, the total of these energies stays the same along one streamline. If the fluid climbs higher, for example, it uses some of its energy as height so its pressure or speed must drop to keep the balance.
Of course, in the real world, things are not perfect. Fluids have viscosity, which causes some energy to be lost as heat or friction. That means energy is not conserved perfectly, but Bernoulli’s Equation still gives us a powerful way to understand fluid flow.
Later, we will also look at the other assumptions that this equation is based on.
Bernoulli’s equation tells us that along a streamline, the three types of pressure, static pressure (push of the fluid), dynamic pressure (energy from motion) and hydrostatic pressure (due to height) all balance in a constant way.
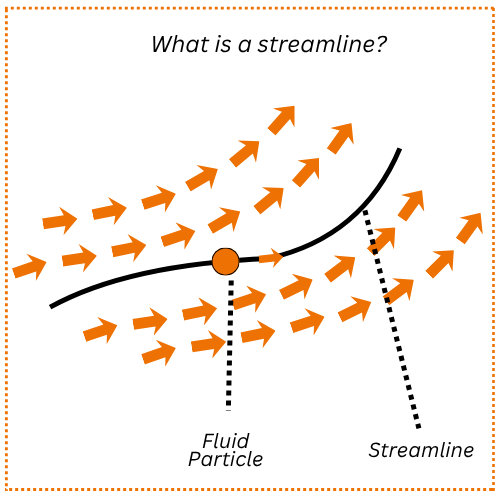
But wait, what exactly is a streamline?
Think of it like an invisible path that a tiny drop of fluid follows as it moves.
In steady flow where the fluid pattern does not change with time, every particle travels smoothly along its own path.
That path is what we call a streamline. See above image.
Most of the time, we use Bernoulli’s equation to compare what happens at two different points along the same streamline. In simple words, it helps us see how the pressure, velocity, and height of a fluid at one point are related to the pressure, velocity, and height at another point.
When written in this way, the equation looks like this:
Let us take an Example – Hosepipes and Venturi Meters
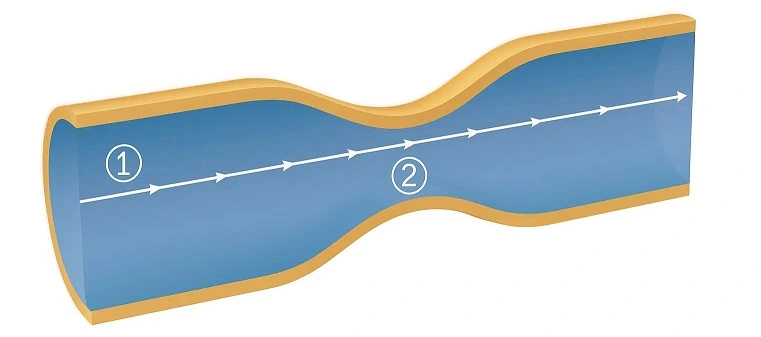
Let us consider an example of water flowing through a hosepipe that has a restriction. We want to find out how the pressure changes between Point 1 and Point 2, which lie on the same streamline.
Since the elevation of both points is practically the same (h₁ = h₂), we can ignore the height terms in Bernoulli’s equation.
This allows us to rearrange the equation and directly calculate the pressure difference between the two points.
Because the fluid is incompressible, the amount of fluid flowing in must equal the amount flowing out.
This means the mass flow rate at Point 1 and Point 2 has to be the same. In other words, the flow is continuous what enters the pipe also leaves it.
After rearranging, we find that the velocity at Point 2 is simply the same velocity at Point 1 multiplied by the ratio of the cross-sectional areas at the two points.
By plugging this velocity relationship into the pressure difference formula, we can now calculate the pressure change using only four things: the velocity at Point 1 (V₁), the area at Point 1 (A₁), the area at Point 2 (A₂), and the fluid’s density (ρ).
Since the pipe becomes narrower at Point 2, the area there (A₂) is smaller than at Point 1 (A₁). This makes the fluid speed up as it passes through the restriction, but at the same time, the pressure drops.
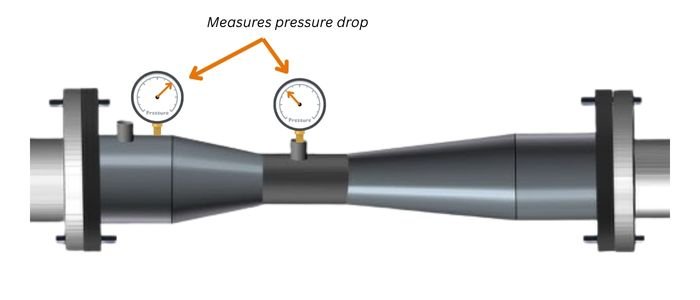
This principle is exactly what a Venturi meter uses to measure flow. By recording the pressure difference between the wider section (P₁) and the narrow section (P₂), and then applying Bernoulli’s equation, the flow rate of the fluid can be calculated.
Different forms of Bernoulli’s equation formula
Bernoulli’s equation formula can be written in three ways, depending on whether the terms are expressed as energy, pressure, or head (distance). The version we saw earlier was the pressure form.
All three forms describe the same idea that energy is conserved along a streamline.
The difference is only in how the energy is expressed.
The choice of which form to use depends on what you want to calculate: energy, pressure, or head.


Frequently Asked Questions about Bernoulli’s Equation
Q1. What does Bernoulli’s Equation explain?
Bernoulli’s Equation explains how the pressure, velocity and height of a fluid are related as it flows. It shows that the total energy of the fluid remains constant along a streamline.
Q2. Why does fluid speed up in a narrow pipe?
When a pipe becomes narrower, the same amount of fluid must pass through a smaller area. To keep the flow continuous, the fluid speeds up, and according to Bernoulli’s principle, its pressure drops.
Q3. Where is Bernoulli’s Equation used in real life?
It is used in designing Venturi meters for flow measurement, aircraft wings to explain lift, pumps and turbines, and even in predicting water supply pressure in pipelines.
Q4. What are the assumptions behind Bernoulli’s Equation?
- Fluid is incompressible.
- Flow is steady (doesn’t change with time).
- No energy is lost due to friction.
- Flow follows a streamline.
Q5. What is the difference between static, dynamic, and hydrostatic pressure?
- Static pressure: The natural push of the fluid.
- Dynamic pressure: The energy due to motion of the fluid.
- Hydrostatic pressure: The effect of the fluid’s height or elevation.
Thats it ! If you want to explore more knowledge, please read my article 100 Essential Engineering Formulas.
I hope you like above blog. There is no cost associated in sharing the article in your social media. Thanks for reading!! Happy Learning!!